『シーケンサなら計算も簡単でしょ?』
使用者にとって、中身がパソコンだろうがシーケンサだろうが基盤だろうが
コンピュータなのだから、計算はお手の物!
なんて考えているのでしょうね、きっと
何かと面倒くさいラダーでの計算を、ポイントを絞って見て行きましょう。
どうも!ずぶです。 今回は シーケンサのラダーでの演算、計算
※四則演算の説明は、特にはしません。
ポイント
ラダーで、演算を行うに当たってのポイントは、2つ
箱の大きさ
その中身
これらを念頭に、演算式を構築して行けば良かったのですね。
復習がてら、それぞれの意味を考えてみましょう。
箱の大きさ
計算を行うには、数値を扱える入れ物 が必要でしたね。
その為に、Dレジスタ 等を用意してくれています。
まずは、レジスタにどの位の数値が入るのかをおさらいしましょう。
1ワード 16ビットに格納できる数値は
10進数 -32,768~32,767
16進数 0000h~FFFFh
2ワード 32ビットの場合は
10進数 -2,147,483,648~2,147,483,647
16進数 00000000h~FFFFFFFFh
の数値が格納できるのでした。
マニュアルにはこのように記載されています。

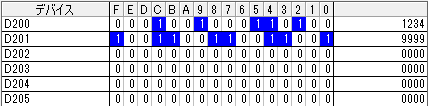
実際に数値を入れ込むとこんな感じ
10進数の場合

16進数の場合

勿論、2ワード だと更に数値が入るのですが
結局、数値の限界 とは 箱の限界 に他なりません。
閑話
ご覧のように、マイナス表記は2の補数になっています。
補数自体は、コンピュータの都合になりますので、一般の計算では、特に補数を気にする必要はありません。
符号付き10進数の場合、最上位にビットが立っていたらマイナスだ。位の認識で十分です。
他の中身
先程の説明に出てきたのは、bin形式 の 10進定数、16進定数 でした。
頭に K とか H とかつける、いつもの奴です。
他にも計算で使う物としては、BCD と 実数 がありましたね。
BCD
0000~9999
4ケタの10進数 を格納しています。
普段は、16進定数のフリをしています。
実数定数
2^-126~2^128
通常で 2ワード占有 している、浮動小数点データ の事です。
小数点を基点に勝手に計算 してくれるので、計測器などが相手の場合は重宝します。
2^128 なんて難しげに書いていますが、
桁数 10の±38乗 って事です。
ちなみに、10の±38乗って、この位
-100000000000000000000000000000000000000
~
100000000000000000000000000000000000000
とにかく、たくさんって事です(笑)
同じダブルワードでも bin の10進数表示だと
2,147,483,647 でしたよね。
じゃあ、全ての計算を実数でやりゃ良いじゃん!と考えますが
精度が出ません。
そりゃ、同じ箱を使ってやり繰りしてるのですから、こっちを立てたらあっちが立たなくなりますよね。
マニュアルを見てみましょう。

単精度の場合、このような形で格納されています。
仮数部 に リアルな数値 を格納して、指数部 は 桁数表示 に使用しているという事です。
仮数部23ビットを10進数で表すと、有効桁数 は 7ケタ となります。
1.234567 × 100000000000000000000000000000000000000
こういう事ですから、扱える範囲は大きくても精度が悪い のですね。
先ほどの、ダブルワード10進と比べると
32bit vs 23bit+桁数
となり、これがそのまま精度の差となるのです。
ちなみに、8ケタ目が四捨五入 されます。
それぞれ見てきましたが、
正確に範囲を覚えてね、といった類のものではありません。
忘れたらマニュアルを見れば良いだけです。
覚えて欲しいのは、たった1点
扱うデータによって、格納形式が違う
これだけです。
こちらも参照
乗算除算
四則演算 の説明はしないと書きましたが、
入れ物の把握には 乗除算 を考えると分かり易いので、ついでに動きだけ再確認してみましょう。
乗算
掛け算の事ですよね。読み方はジョウザン
ヘルプより

1ワード × 1ワード = 2ワード
って事ですよね。
先程の最大値 32,767 が放り込まれた場合、
32,767 × 32,767 = 1,073,676,289
このようになりますから、答えには 2ワード の用意が必要だよって事ですね。
解は 2ワード と言えど、1ワードで収まる解なら [ MOV ] で飛ばして 下位の1ワード だけを使いまわす事も日常茶飯事。

演算したものを、表示エリアに飛ばしたりとかですね。
除算
割り算の事ですよね。読み方はジョザン
ヘルプより

1ワード ÷ 1ワード = 2ワード
乗算と同じく、解は 2ワード なのですが、
商1ワード 余り1ワード に格納されます。
最大値 32,767 が放り込まれた場合、
32,767 ÷ 1 = 商 32,767 余り 0
1 ÷ 32,767 = 商 0 余り 32,767
このようになりますから、答えは 商と余り 1ワード ずつで良いのですね。
0 で割るとエラー になりますから、注意が必要でした。
計算をしてみよう
それでは、先程までのおさらいを元に、実際に計算をしてみましょう。
※お使いのシーケンサで、命令語の違いはあるかもしれませんが、適当に読み替えて下さいね。
まずは、普通の掛け算です。

割って戻してみましょう

戻らなくなっちゃいました。
掛け算の解が、32767 を超えているので、D10 は 2ワード で正しい値を持っているのでしたね。
ならば、D10 を ダブル で割ってみましょう。

ぐちゃぐちゃになっちゃいました(笑)
ダブルにした事で、被除数 と 除数 両方をダブルと認識 しますから、
除数が D0+D1 の 2ワードで割った 事になったのですね。
ならばならば、使用エリアを離してみましょう。
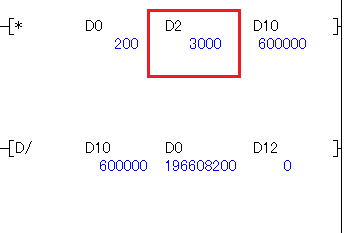
D0 が戻りませんね
先程使用した D1 にゴミが残っているのですね。
ならば×3、D0 をダブルに変更しましょう。

デバイスや、タッチパネルからのデータを加工する時に起こり得る状況ですね。
先もって箱の大きさを把握しておくことで、こういう事態に陥らないような工夫も出来るようになるのです。
BCDの計算
先程の結果 D12 に対して、BCD の掛け算 をしてみましょう。
まずは、データ形式が違う ので、形式合わせが必要です。
BCD は、16進定数の仲間ですから、定数の場合は頭に H を付ければ良かったのですね。
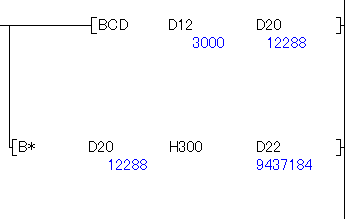
D22 の値が凄い事になっていますが、今回は、ぐちゃぐちゃになっている訳ではありません。
表示形式を切り替えます。
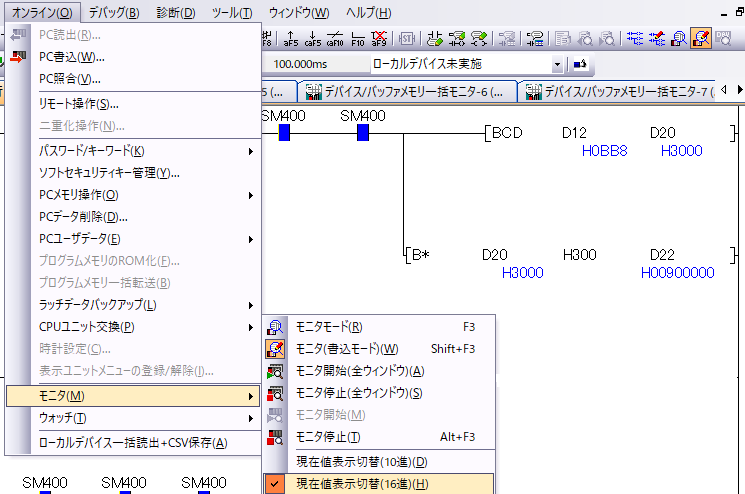
正しく表示されました。
掛け算だったので、解が BCD2ワード となっていたのですね。
解はダブルですので、 D22 + D23 は
0090 0000 h
このように格納されています。
つまり、
D22 から ダブル の視点で見れば、900000h
D23 から シングル の視点で見れば、90h
が格納されているように見える訳です。
試しに、上位の D23 だけを抜いてみましょう。
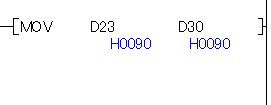
実数の計算
先程抜いた D30 に対して、実数の足し算をしてみましょう。
データ形式が違う ので、形式合わせが必要でしたね。
BCD から実数変換の命令は無いので、一度 BIN に変換した後 実数 に変換します。

実数定数は、頭に E を付けるのでしたね。

計算が終わったら、bin に戻して扱いやすい形にしてあげると良いですね。

binは少数点を扱わないので、少数点以下は無かった事になっちゃいました。
中身の形式を把握しておかなければ、予期しない演算結果になるのは想像できるかと思います。
演算時のデータミス等を防ぐ為に、コメント等が有効なのですが、ついつい忘れがち。
演算を通す為に四苦八苦して、それどころでは無いのは分かるのですが、例えば、INT や BCD などデータ形式だけをコメントに書くだけでも、デバッグや修正が随分変わってきます。
まとめ
ラダーでの計算は、全てを想定してコードを書くと、ガチャガチャと面倒くさい事になりがちです。
けれど、箱のサイズと中身さえ把握しておけば、入れて欲しくない数値をタッチパネルで誘導したり、小技を効かせて弾くなんて事も出来ます。
実際、ゴミ避けで DBL に変換など書きませんしね(笑)
計算に受け身になるのではなく、シンプルなコードに誘導するにはどこを使うか等を考えると、楽しくなるかもしれませんよ。
合わせて読みたい

最近のコメント